Reconnaissance de chiffres manuscrits sur Python

Implémentation d'un programme de reconnaissance de chiffres manuscrits sur Python

Dernière mise à jour le Jun 16, 2022 20 min de lecture Demo

Image credit: Josef Steppan

Dans l’image ci-dessus, chaque chiffre a sa représentation sous forme d’une image ainsi que son étiquette correspondante. Par exemple, le premier chiffre en bas à gauche a une étiquette égale à 9 vu qu’il s’agit bien du chiffre 9. Cette image est un aperçu de la base de données MNIST pour Modified ou Mixed National Institute of Standards and Technology qui est une base de données de chiffres écrits à la main. Il s'agit d'une base de référence qui sert notamment à tester et comparer des algorithmes d'apprentissage statistique. L'objectif est de déterminer le chiffre écrit sur chaque image (problème de classification d'images). La base MNIST se compose de 60 000 images d'apprentissage et 10 000 de test. Par ailleurs, la représentation des chiffres est normalisée à travers tout le jeu de données. Ainsi, chaque chiffre est codé dans un format 8 pixels x 8 pixels, chaque pixel pouvant prendre une valeur comprise entre 0 et 255. Ainsi, cette plage de valeurs représente le niveau de gris Grayscale. Autrement dit, chaque représentation d’une image est une matrice de dimension 8 x 8. Le jeu de données MNIST présent par défaut dans la librairie scikit-learn comporte un sous-ensemble de la “vraie” base de données MNIST. Dans ce tutoriel, l'objectif sera de se baser d'une part sur la descente de gradient et la descente de gradient stochastique stochastique utilisée pour l'estimation des paramètres du modèle de régression multinomiale afin de reconnaitre les images de l'ensemble de test au regard des chiffres manuscrits dèjà vus lors de la phase d'entrainement du modèle et d'autre part sur l'utilisation du framework keras pour mettre en oeuvre la régression multinomiale ainsi que le réseau de neurones convolutionnel inspiré de LeNet-5.

1. Données MNIST

Nous commençons d’abord par importer les librairies nécessaires.

import numpy as np
import pandas as pd
from matplotlib import pyplot as plt
import random
import time
from keras.datasets import mnist

La base de données se télécharge facilement avec le package keras comme suit :

(X0, Y0), (X1, Y1) = mnist.load_data()

Dans cette importation, $X_0$ et $X_1$ sont des bases d'images d'apprentissage et de test, respectivement. Ce sont des numpy.ndarray de taille $n \times 28 \times 28$, où $n=60000$ pour $X_0$ et $n=10000$ pour $X_1$.

$X_0(i, :, :)$ est la $i^{ème}$ image de la base d’apprentissage ; elle est de taille $28 \times 28$. On peut l’afficher avec la fonction imshow de matplotlib.pyplot. Les variables $Y_0$ et $Y_1$ contiennent les classes des observations dans chacune des bases. Les classes sont étiquetées de $0$ à $9$.

Avant toute analyse, on va préparer les données de la manière suivante :

# On met le type des images en float.
X0 = X0.astype('float32')
X1 = X1.astype('float32')
# On met les images sous la forme d'un vecteur.
X0 = X0.reshape(60000, 784)
X1 = X1.reshape(10000, 784) 
# On normalise les images.
X0 = X0 / 255.0
X1 = X1 / 255.0

Nous pouvons alors afficher l’une des images.

#Affichage de la 3ème image
n = 2
Y0_ = pd.get_dummies(Y0).values
Y1_ = pd.get_dummies(Y1).values
plt.imshow(X0[n, :].reshape(28, 28), cmap="gray")

2. Régression multinomiale

La régression multinomiale est un modèle de classification qui étend la régression logistique lorsque le nombre de classes possibles est supérieur à 2. Le modèle est le suivant. On décrit la classe d'un individu au moyen d'une variable aléatoire $Y$ à valeurs dans un ensemble discret $\{1,\cdots, K\}$ représentant des étiquettes de classe. Pour chaque individu, on dispose de variables $x$ (dites de régression) dans $\mathbb{R}^p$. On suppose que la distribution de probabilités de $Y$ dépend de $x$ et d'un ensemble $\theta = (\theta^{(k)})_{k=1}^K$ de $K$ vecteurs de paramètres inconnus $\theta^{(k)}$ dans $\mathbb{R}^{p+1}$ selon le modèle "soft-max"

\begin{equation} \label{eqn:softmax_proba} \forall k \in {1,\cdots, K}, \mathbb{P}(Y = k) = \frac{\exp(\langle \theta^{(k)}, \tilde{x} \rangle )}{\sum_{m=1}^K \exp(\langle \theta^{(m)}, \tilde{x} \rangle )},\mathrm{avec} \tilde{x} = \left( \begin{array}{c} 1 \ x \end{array} \right). \end{equation}

Les estimateurs du maximum de vraisemblance de l’échantillon sont les paramètres $\theta$ qui minimisent le critère d’entropie croisée: \begin{equation} \label{eqn:entropiecroisee} \mathcal{S}(\theta) = - \frac{1}{n} \sum_{i=1}^n \sum_{k=1}^K z_i^{(k)} \log\left(p_i^{(k)}(\theta) \right),\end{equation} avec \begin{equation} z_i^{(k)} = \mathbf{1}_{y_i = k} \mathrm{et} p_i^{(k)}(\theta) = \frac{\exp(\langle \theta^{(k)}, \tilde{x}_i \rangle )}{\sum_{m=1}^K \exp(\langle \theta^{(m)}, \tilde{x}_i \rangle )}. \end{equation}

3. Descente de gradient

Une descente de gradient est un algorithme itératif permettant de minimiser une application différentiable $\mathcal{S}$ par rapport à un ensemble de variables $\theta$. Dans la descente de gradient à pas fixe, la mise à jour des variables $\theta$ s'écrit à chaque itération :

\begin{equation} \label{eqn:miseajour} \theta \longleftarrow \theta - \rho \nabla_{\theta} \mathcal{S}(\theta), \end{equation} où $\rho>0$ désigne un pas fixe et $\nabla_{\theta} \mathcal{S}$ le gradient de $\mathcal{S}$ par rapport à $\theta$.

Le gradient de l’entropie croisée $\mathcal{S}$ par rapport à $\theta^{(k)}$ en $\theta$ vaut : $$ \nabla_{\theta^{(k)}} \mathcal{S}(\theta) = \frac{1}{n} \sum_{i=1}^{n} \left(p_i^{(k)}(\theta) - z_i^{(k)}\right) \tilde{x}_i . $$

3. Application de l’algorithme de descente de gradient sur les données MNIST

Après avoir défini les fonctions qui interviennent dans le calcul du gradient, l'application de l'algorithme de descente de gradient, nous pouvons définir la fonction qui effectue l'algorithme de descente de gradient pour la régression multinomiale.

def RegMultinomialGradDesc(X_train, Y_train, X_test, Y_test, Y_train_list, Y_test_list, epochs, alpha):
    """
    Calcul du gradient, theta et entropie croisée

    Paramétres
    ----------
    X_train : ndarray (n x p)
    Y_train : ndarray (n x K)
    epochs : nombre d'epoques à réaliser
    alpha : scalaire
    X_test : ndarray (m x p)
    Y_test : ndarray (m x K)
   
    Returns
    -------
    beta : ndarray (p+1 x K)
    Lvals_train : liste contenant les valeurs de l'entropie sur les données de train à toutes les epoques
    Lvals_test : liste contenant les valeurs de l'entropie sur les données de validation à toutes les epoques
    Learning_T : liste contenant les temps d'exécution des époques
    scores_train : liste contenant les scores sur les données de train à toutes les époques
    scores_test : liste contenant les scores sur les données de validation à toutes les époques
    """ 
    Epochs = epochs
    N, p = X_train.shape
    X_train = np.insert(X_train, 0, 1, axis=1) # on insère des 1 à la position 0 (colonne 0) de X
    X_test = np.insert(X_test, 0, 1, axis=1) # on insère des 1 à la position 0 (colonne 0) de X
    K = Y_train.shape[1]
    Theta = np.zeros((p+1, K))
    Z_train = X_train[:, 1::]
    Z_test = X_test[:, 1::]
    Learning_T = []
    Lvals_train = []
    Lvals_test = []
    scores_train = []
    scores_test = []
    
    for epoch in range(Epochs):
        start_time = time.time() 
        L_train = eval_L(X_train, Y_train, Theta)
        L_test = eval_L(X_test, Y_test, Theta)
        Lvals_train.append(L_train)
        Lvals_test.append(L_test)
        
        print("Epoch " + str(epoch) + " : " + " Cost train est : " + str(L_train) + " et" + " Cost test est : " + str(L_test))
        
        Theta = Theta - (1/N)*alpha*Gradient(X_train, Y_train, Theta)
        
        prediction_Xtrain  = prediction_Label(Z_train, Theta)
        
        numClassCorrect_train = 0
        for i in range(N):
            if prediction_Xtrain[i]==Y_train_list[i]:
                numClassCorrect_train+=1
            accuracy_train = numClassCorrect_train/N
        scores_train.append(accuracy_train)
        
        prediction_Xtest  = prediction_Label(Z_test, Theta)
        N_test = Z_test.shape[0]
        
        numClassCorrect_test = 0
        for i in range(N_test):
            if prediction_Xtest[i]==Y_test_list[i]:
                numClassCorrect_test+=1
            accuracy_test = numClassCorrect_test/N_test
        scores_test.append(accuracy_test)
        
        learning_time = time.time() - start_time  
        Learning_T.append(learning_time)
        
    return Theta, Learning_T, Lvals_train, Lvals_test, scores_train, scores_test

alpha = 0.01 # fixation du pas
epochs = 100 # fixation du nombre d'epochs
X_train = X0[:50000]
Y_train = Y0_[:50000] # Y sous forme d'une matrice n, K
X_test = X1
Y_test = Y1_
Y_train_list = Y0[:50000] # Y sous forme d'une liste de longueur n
Y_test_list = Y1
Theta, Learning_T, entrop_train, entrop_test, score_train, score_test = RegMultinomial_GradDesc(X_train, Y_train, X_test, Y_test, Y_train_list, Y_test_list, epochs, alpha)

Appliquons l’algorithme de descente de gradient sur les données MNIST en prenant 50000 données d’apprentissage et 10000 de validation.

alpha = 0.01 # fixation du pas
epochs = 100 # fixation du nombre d'epochs
X_train = X0[:50000]
Y_train = Y0_[:50000] # Y sous forme d'une matrice n, K
X_test = X1
Y_test = Y1_
Y_train_list = Y0[:50000] # Y sous forme d'une liste de longueur n
Y_test_list = Y1
Theta, Learning_T, entrop_train, entrop_test, score_train, score_test = RegMultinomial_GradDesc(X_train, Y_train, X_test, Y_test, Y_train_list, Y_test_list, epochs, alpha)

epoch = range(epochs)
plt.figure("")
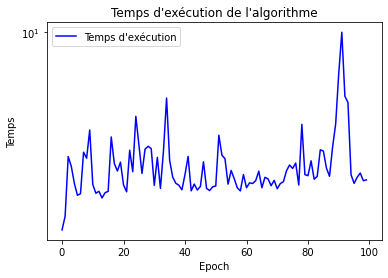
plt.title("Temps d'exécution de l'algorithme")
plt.xlabel("Epoch")
plt.ylabel("Temps")
plt.yscale('symlog')
plt.plot(epoch, Learning_T, label = "Temps d'exécution", color='blue')
plt.legend()

epoch = range(epochs)
plt.figure("")
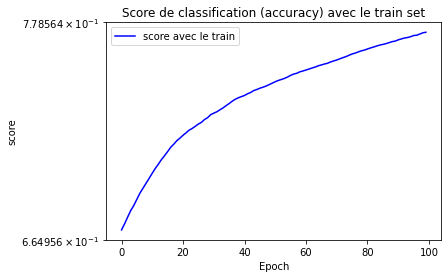
plt.title("Score de classification (accuracy) avec le train set")
plt.xlabel("Epoch")
plt.ylabel("score")
plt.yscale('symlog')
plt.plot(epoch, score_train, label = "score avec le train", color='blue')
plt.legend()

epoch = range(epochs)
plt.figure("")
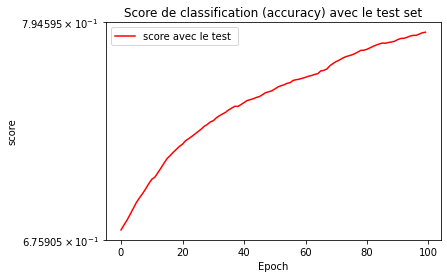
plt.title("Score de classification (accuracy) avec le test set")
plt.xlabel("Epoch")
plt.ylabel("score")
plt.yscale('symlog')
plt.plot(epoch, score_test, label = "score avec le test ", color='red')
plt.legend()

4. Descente de gradient stochastique par mini-lots

L'algorithme de gradient stochastique est une modification de l'algorithme du gradient qui consiste à prendre un seul exemple d'apprentissage au hasard pour mettre à jour le paramètre $\theta$ à chaque époque. On s'intéresse ici à une variante de l'algorithme de gradient stochastique qui fait ces mises à jour en prenant une série de mini-lots (batchs) d'exemples d'apprentissage tiré au hasard. Pour cet algorithme, le gradient de l'entropie croisée $\mathcal{S}$ s'écrira $$ \nabla_{\theta^{(k)}} \mathcal{S}(\theta) = \frac{1}{m} \sum_{i \in B_j} \left(p_i^{(k)}(\theta) - z_i^{(k)}\right) \tilde{x}_i, $$ où $B_j$ est un ensemble qui regroupe $m$ indices d'un jème lot d'observations pris au hasard. Une époque de l'algorithme consistera en une série de plusieurs mises à jour faisant intervenir différents lots. Le nombre de mises à jour pour une époque pourra par exemple être fixé à $\lfloor n / m \rfloor$. La descente de gradient ordinaire est un cas particulier de la descente de gradient stochastique lorsque l'on fixe $m=n$.

Modifions de l'algorithme précédent afin d'inclure des mises à jour sur mini-lots et appliquons le aux données MNIST.

Définissons d’abord la fonction qui calcule le gradient par mini-lots.

def Gradient_miniLot(X, Y, Theta, m):
    N, p = X.shape
    K = Y.shape[1]
    #m = 256
    Gradient = np.zeros((p, K))
    T = range(N)
    random.seed(10)
    Bj = random.sample(T, int(m))
    for i in Bj:
        XiHat = X[i]
        XiHat = XiHat.reshape(1, XiHat.shape[0])
        Yi = Y[i]
        Yi = Yi.reshape(1, Yi.shape[0])
        qi = Soft_Max(XiHat, Theta)
        Gradient += np.outer(XiHat, qi - Yi)
    return Gradient

Nous pouvons maintenant définir celle qui inclut les mini-lots.

def RegMultinomial_GradDescMinibatch(X_train, Y_train, X_test, Y_test, Y_train_list, Y_test_list, alpha, m):
    """
    Calcul du gradient, theta et entropie croisée

    Parameters
    ----------
    X_train : ndarray (n x p)
    Y_train : ndarray (n x K)
    epochs : nombre d'epoques à réaliser
    alpha : scalaire
    m : nombre de lots
    X_test : ndarray (m x p)
    Y_test : ndarray (m x K)
   
    Returns
    -------
    beta : ndarray (p+1 x K)
    Lvals_train : liste contenant les valeurs de l'entropie sur les données de train à toutes les epoques
    Lvals_test : liste contenant les valeurs de l'entropie sur les données de validation à toutes les epoques
    Learning_T : liste contenant les temps d'exécution des époques
    scores_train : liste contenant les scores sur les données de train à toutes les époques
    scores_test : liste contenant les scores sur les données de validation à toutes les époques
    """ 
    N, p = X_train.shape
    Epochs = int(N/m)
    X_train = np.insert(X_train, 0, 1, axis=1) # on insère des 1 à la position 0 (colonne 0) de X
    X_test = np.insert(X_test, 0, 1, axis=1) # on insère des 1 à la position 0 (colonne 0) de X
    K = Y_train.shape[1]
    Theta = np.zeros((p+1, K))
    Z_train = X_train[:, 1::]
    Z_test = X_test[:, 1::]
    Learning_T = []
    Lvals_train = []
    Lvals_test = []
    scores_train = []
    scores_test = []
    
    for epoch in range(Epochs):
        start_time = time.time() 
        L_train = eval_L_minibatch(X_train, Y_train, Theta, m)
        L_test = eval_L_minibatch(X_test, Y_test, Theta, m)
        Lvals_train.append(L_train)
        Lvals_test.append(L_test)
        
        print("Epoch " + str(epoch) + " : " + " Cost train est : " + str(L_train) + " et" + " Cost test est : " + str(L_test))
        
        Theta = Theta - (1/N)*alpha*Gradient_miniLot(X_train, Y_train, Theta, m)
        
        prediction_Xtrain  = prediction_Label(Z_train, Theta)
        
        numClassCorrect_train = 0
        for i in range(N):
            if prediction_Xtrain[i]==Y_train_list[i]:
                numClassCorrect_train+=1
            accuracy_train = numClassCorrect_train/N
        scores_train.append(accuracy_train)
        
        prediction_Xtest  = prediction_Label(Z_test, Theta)
        N_test = Z_test.shape[0]
        
        numClassCorrect_test = 0
        for i in range(N_test):
            if prediction_Xtest[i]==Y_test_list[i]:
                numClassCorrect_test+=1
            accuracy_test = numClassCorrect_test/N_test
        scores_test.append(accuracy_test)
        
        learning_time = time.time() - start_time  
        Learning_T.append(learning_time)
            
    return Theta, Learning_T, Lvals_train, Lvals_test, scores_train, scores_test

Application de l’algorithme de descente de gradient stochastique par mini-lots sur les données MNIST en prenant 50000 données d’apprentissage et 10000 de validation.

alpha = 0.01 # fixation du pas
m = 256 # fixation du nombre d'epochs
X_train = X0[:50000]
Y_train = Y0_[:50000] # Y sous forme d'une matrice n, K
X_test = X1
Y_test = Y1_
Y_train_list = Y0[:50000] # Y sous forme d'une liste de longueur n
Y_test_list = Y1
Theta, Learning_T, entrop_train, entrop_test, score_train, score_test = RegMultinomial_GradDescMinibatch(X_train, Y_train, X_test, Y_test, Y_train_list, Y_test_list, alpha, m)

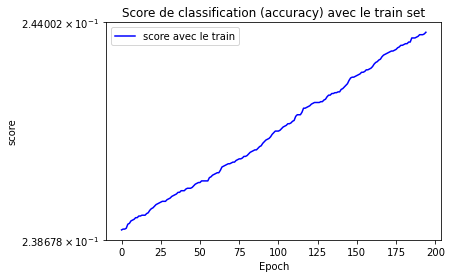
plt.figure("")
plt.title("Score de classification (accuracy) avec le train set")
plt.xlabel("Epoch")
plt.ylabel("score")
plt.yscale('symlog')
plt.plot(epoch, score_train, label = "score avec le train", color='blue')
plt.legend()

plt.figure("")
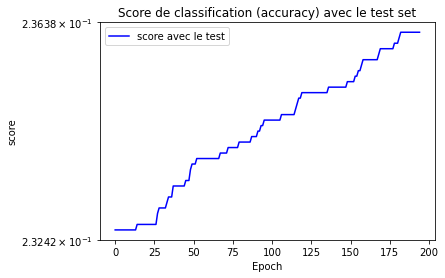
plt.title("Score de classification (accuracy) avec le test set")
plt.xlabel("Epoch")
plt.ylabel("score")
plt.yscale('symlog')
plt.plot(epoch, score_test, label = "score avec le test", color='blue')
plt.legend()

5. Régression multinomiale en keras

Ici, nous allons mettre en oeuvre en keras le modèle de régression multinomiale.

# Importation des librairies nécessaires
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import tensorflow as tf
from tensorflow import keras
from tensorflow.keras.models import Sequential 
from tensorflow.keras.layers import Dense, Activation
from keras.regularizers import l2

# Training set et test set
(X0, Y0), (X1, Y1) = tf.keras.datasets.mnist.load_data()

# On met les images sous la forme de vecteur.
X0 = X0.reshape(60000, 784)
X1 = X1.reshape(10000, 784) 
# On normalise les images.
X0 = X0 / 255.0
X1 = X1 / 255.0

# Transformation de Y0 en matrice N X K avec N le nompbre d'observations et K le nombre de classes
Y0_ = pd.get_dummies(Y0).values

# Constitution d'un ensemble d'entrainement composé de 50000 observations 
# et d'un ensemble test composé de 10000 observations
X_train = X0[:50000]
Y_train = Y0_[:50000]
X_valid = X0[:20000]
Y_valid = Y0[:20000]
X_test = X1
Y_test = Y1

Nous pouvons dès à présent construire le modèle de régression multinomiale sous keras.

# Variables et classes du modèle
input_dim = X_train.shape[1] # 784 variables
output_dim = Y0_.shape[1] # 10 classes

# Construction du modèle de régression multinomiale
def classification_model():
    model = Sequential()
    model.add(Dense(output_dim, input_dim=input_dim, activation='softmax'))
    model.compile(loss='categorical_crossentropy', optimizer='sgd', metrics=['accuracy'])
    return model

# Entrainement du modèle
keras_model = classification_model()
keras_model.fit(X_train, Y_train, epochs=300, verbose=0)

Qu’en est-il de la performance du modèle sur les données de validation?

# Calcul du degré de précision ou accuracy sur X_valid
classes = np.argmax(keras_model.predict(X_valid), axis = 1)
N_valid = X_valid.shape[0]
numClassCorrect = 0
for i in range(N_valid):
    if classes[i]==Y_valid[i]:
        numClassCorrect+=1
        
accuracy = numClassCorrect/N_valid
print('Accuracy sur X_valid : ' + str(accuracy))

Accuracy sur X_valid : 0.9348

Nous obtenons un score de 93%, ce qui est quand même réconfortant en attendant de voir ce qui se passe si le modèle reçoit les données qu'il n'a jamais vues.

Allons voir la précision sur les données test.

# Prédictions de X_test
classes = np.argmax(keras_model.predict(X_test), axis = 1)
classes.shape

  (10000,)

# Calcul du degré de précision ou accuracy sur X_test
N_test = X_test.shape[0]
numClassCorrect = 0
for i in range(N_test):
    if classes[i]==Y_test[i]:
        numClassCorrect+=1
        
accuracy = numClassCorrect/N_test
print('Accuracy sur X_test : ' + str(accuracy))

Accuracy sur X_test : 0.9254

Ici également nous obtenons une bonne précision, légèrement inférieure à celle obtenue sur les données de validation.

Voyons maintenant la différence si on apprend le modèle sur un ensemble train réduit. Prenons N_train = 1000 par exemple.

X_train = X0[:1000]
Y_train = Y0_[:1000]
X_valid = X0[:400]
Y_valid = Y0[:400]

# Entrainement du modèle
keras_model = classification_model()
keras_model.fit(X_train, Y_train, epochs=300, verbose=0)

# Calcul du degré de précision ou accuracy sur X_valid
classes = np.argmax(keras_model.predict(X_valid), axis = 1)
N_valid = X_valid.shape[0]
numClassCorrect = 0
for i in range(N_valid):
    if classes[i]==Y_valid[i]:
        numClassCorrect+=1
        
accuracy = numClassCorrect/N_valid
print('Accuracy sur X_valid : ' + str(accuracy))

Accuracy sur X_valid : 0.9675

# Prédictions de X_test
classes = np.argmax(keras_model.predict(X_test), axis = 1)
classes.shape

(10000,)

# Calcul du degré de précision ou accuracy sur X_test
N_test = X_test.shape[0]
numClassCorrect = 0
for i in range(N_test):
    if classes[i]==Y_test[i]:
        numClassCorrect+=1
        
accuracy = numClassCorrect/N_test
print('Accuracy sur X_test : ' + str(accuracy))

Accuracy sur X_test : 0.8662

Avec un ensemble d'apprentissage très réduit, on obtient une précision plus faible sur les données test. En revanche, la précision sur les données de validation a augmenté d'environ 3% dans des proportions égales (dans les deux expériences). Ce phénomène laisse présager de l'overvitting sinon cela peut être dû à l'insuffisance de données d'entrainement.

Maintenant que nous avons vu que le score de classification a baissé si on passe d'un ensemble de train grand (50000) à un ensemble de train réduit (1000) soit une baisse de 5% (92% à 87%) avec un nombre d'epoques assez élevé (300), nous pouvons voir comment varie ce score en fonction du nombre d'epoques.

Pour des soucis de puissance de calcul de nos ordinateurs, nous pouvons nous limiter à 30 époques afin de voir cette variation de score.

accuracy_mnist = []
for i in range(1, 31):
    # Entrainement du modèle
    keras_model = classification_model()
    keras_model.fit(X_train, Y_train, epochs=i, verbose=0)
    
    # Prédictions de X_test
    classes = np.argmax(keras_model.predict(X_test), axis = 1)
    classes.shape
    
    # Calcul du degré de précision ou accuracy sur X_test
    N_test = X_test.shape[0]
    numClassCorrect = 0
    for i in range(N_test):
        if classes[i]==Y_test[i]:
            numClassCorrect+=1

    accuracy = numClassCorrect/N_test
    accuracy_mnist.append(accuracy)

epoque = range(1, 31)
plt.title("Score de classification en fonction du nombre d'époque")
plt.xlabel("Epoch")
plt.ylabel("Score")
plt.yscale('symlog')

plt.plot(epoque, accuracy_mnist)

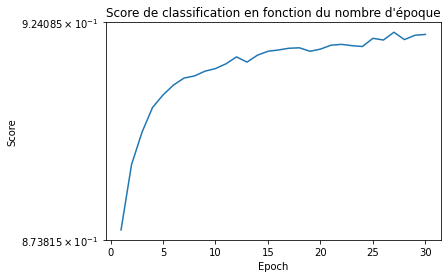
print(accuracy_mnist.index(max(accuracy_mnist)))

L'analyse de ce graphique montre que le score de classification augmente au fur et à mesure que le nombre d'epoques augmente. Néanmoins à partir de 25 époques, le score n'augmente presque pas et connait de légères fluctuations. Le score maximal est atteint pour un nombre d'epoques égal à 26.

Nous allons maintenant mettre en oeuvre en Keras le réseau de neurones convolutionnel inspiré de LeNet-5 dont les couches sont décrites dans le tableau ci-dessous.

Type	Cartes	Noyau	Pas	Activation
Conv.	6	5x5	1	tanh
Av. Pooling	6	2x2	2	-
Conv.	12	5x5	1	tanh
Av. Pooling	12	2x2	4	-
Dense	-	10	-	softmax

Dimension des images

Dans le modèle inspiré par LeNet-5, la couche d'entrée est conçue pour des images 32x32. Ensuite, les dimensions de ces images sont passées dans la couche qui suit. Néanmoins avec les données MNIST, nous avons des images de dimensions 28x28. Comme ces dernières ne répondent pas aux normes de la couche d'entrée, on va appliquer le padding sur elles.

Nombre de paramètres à chaque couche

Le réseau de neurones convolutionnel inspiré de LeNet-5 utilise principalement trois types de couches : Conv (pour Convolutional layers), Avg-Pooling (pour Average Pooling) et dense (avec softmax). Conv prend comme paramètres le nombre de filtres, les dimensions du noyau, la taille des données (pour la première couche seulement) et l'activation. La couche dense prend comme paramètre le nombre de neurones de la couche de sortie (nombre de classes, 10 dans le cas de MNIST) et le paramètre activation pour la couche de sortie est le softmax. Pour ce qui est de la couche Avg-Pooling, nous ne lui fournissons aucun paramètre car par défaut certains arguments requis sont initialisés lorsque la couche est appelée sachant que le rôle de cette couche est de sous-échantilloner les cartes d'entités au fur et à mesure qu'elles se déplacent dans le réseau. Il existe également une quatrième couche aplatie appelée flatten qui ne prend aucun paramètre. La première couche Conv produit en sortie 6 cartes de caractéristiques et a une taille de noyau de dimension 5x5. Ainsi les dimensions des 6 cartes produites par la première couche sont 28x28. Ensuite, la première couche Avg-Pooling suit cette première couche. Elle divise par deux la dimension des cartes qu'elle reçoit de la couche qui la précéde d'où le nom de sous-échantillonnage. Par la suite, elle produit 6 cartes, chacune correspondant aux cartes transmises en entrées de la couche précédente. Et le processus continue...

Comparaison avec le modèle dense de la régression multinomiale

Contrairement au modèle dense de la régression multinomiale qui utilise seulement trois paramètres à savoir le nombre de variables, le nombres de classe et l'activation, le réseau de neurones convolutionnel inspiré de LeNet-5 comporte trois types de couches avec ses paramètres. Ces trois types de couches se succèdent une à une en prenant en entrée des images ou des cartes et en fournissant des cartes en sorties. Le processus continue couche après couche et à chaque couche, il y a une fonction d'activation qui est utilisée (tangente hyperbolique et sigmoid) jusqu'à la couche de sortie qui utilise quant à elle le softmax. On voit donc cette complexité (plusieurs couches, paramètres et fonctions d'activation) dans le modèle convolutionnel alors que dans le réseau dense cela devient assez simple.

Application du modèle aux données MNIST et comparaison aux résultats obtenus avec la régression multinomiale.

Une fois les images chargées, nous pouvons les normaliser et les reformater (reshape) afin de facilité l'apprentissage des neurones mais aussi du fait que cela présage de meilleurs résultats.

# Importation des librairies nécessaires
import numpy as np
import mnist
from tensorflow import keras

# Images de train et de test
train_img = mnist.train_images()
train_label = mnist.train_labels()
test_img = mnist.test_images()
test_label = mnist.test_labels()

# Affichage de la dimension des images
print(train_img.shape) ### (60000, 28, 28)
print(train_label.shape) ### (60000,)
print(test_img.shape) ### (60000, 28, 28)
print(test_label.shape) ### (60000,)

(60000, 28, 28)
(60000,)
(10000, 28, 28)
(10000,)

# Normalisation des images. La raison de la normalisation est de s'assurer que l'ensemble
# constitué d'images a une moyenne de 0 et un écart type de 1 (ici nous allons passer de [0, 255] à [-0.5, 0.5]).
#Les avantages de cela se voient dans la réduction du temps d'apprentissage. 
train_img = (train_img / 255) - 0.5
test_img = (test_img / 255) - 0.5

# Reshape des images (car keras exige la troisièeme dimension)
train_img = np.expand_dims(train_img, axis=3)
test_img = np.expand_dims(test_img, axis=3)

print(train_img.shape) ### (60000, 28, 28, 1)
print(test_img.shape)  #### (10000, 28, 28, 1)

(60000, 28, 28, 1)
(10000, 28, 28, 1)

Nous pouvons réserver un ensemble constitué de 5000 observations (ensemble de validation) pour évaluer les performances du réseau à diverses itérations.

valid_img = train_img[:5000] 
valid_label = train_label[:5000]

Dans ce qui suit, nous donnons les dimensions de l'ensemble d'apprentissage en indiquant qu'il y a aura un padding sur les images (pour passer de 28x28 à 32x32). En effet, durant les phases d'entrainement et de validation, les neurones s'attendent à recevoir des images par lots, c'est pour cela nous avons fait un reshape à trois dimensions afin que la dimension supplémentaire soit vue comme représentative du nombre d'images dans un lot.

lenet_5_model = keras.models.Sequential([ 
    keras.layers.Conv2D(6, kernel_size=5, strides=1, activation='tanh', input_shape=train_img[0].shape, padding='same'),  
    keras .layers.AveragePooling2D(), 
    keras.layers.Conv2D(16, kernel_size=5, strides=1, activation='tanh', padding='valid'), 
    keras.layers.AveragePooling2D(), 
    keras.layers.Flatten(), 
    keras.layers.Dense(120, activation='tanh'),  
    keras.layers.Dense(84, activation='tanh'),  
    keras.layers.Dense( 10, activation='softmax') 
])

Compilation et construction du modèle

# Ici, nous compilons le modèle dèjà implémenté en arrière-plan en fournissant des caractéristiques
# supllémentaires : fonction de perte, optimiseur et la métrique
lenet_5_model.compile(optimizer='adam', loss=keras.losses.sparse_categorical_crossentropy, metrics=['accuracy'])

# Nous entrainons le modèle en utilisant une fonction de perte (différence entre valeurs prédites
# par le réseau et les valeurs réelles de l'ensemble d'entrainement), un algorithme d'optimisation 
# (adam) afin de faciliter le nombre de modifications apportées aux poids au sein du réseau, un 
# ensemble de validation à chaque époque.
lenet_5_model.fit(train_img, train_label, epochs=5, validation_data=(valid_img, valid_label))

Nous voyons qu'avec un nombre d'epoques égal à 5, nous atteignons une précision de validation d'environ 99%. Néanmoins, pour être plus explicite, nous allons évaluer les performances du modèle sur des données qu'il n'a jamais vu, le jeu de données test.

# Evaluation sur le jeu de données test
lenet_5_model.evaluate(test_img, test_label)


313/313 [==============================] - 1s 4ms/step - loss: 0.0612 - accuracy: 0.9808
    
[0.06115240976214409, 0.9807999730110168]

L'analyse des résultats obtenus à l'issue de cette évaluation montre une précision de 98%, ce qui est très intéressant.

Voici quelques caractéristiques du modèle par couche.


    Model: "sequential_1"
    _________________________________________________________________
     Layer (type)                Output Shape              Param #   
    =================================================================
     conv2d (Conv2D)             (None, 28, 28, 6)         156       
                                                                     
     average_pooling2d (AverageP  (None, 14, 14, 6)        0         
     ooling2D)                                                       
                                                                     
     conv2d_1 (Conv2D)           (None, 10, 10, 16)        2416      
                                                                     
     average_pooling2d_1 (Averag  (None, 5, 5, 16)         0         
     ePooling2D)                                                     
                                                                     
     flatten (Flatten)           (None, 400)               0         
                                                                     
     dense_1 (Dense)             (None, 120)               48120     
                                                                     
     dense_2 (Dense)             (None, 84)                10164     
                                                                     
     dense_3 (Dense)             (None, 10)                850       
                                                                     
    =================================================================
    Total params: 61,706
    Trainable params: 61,706
    Non-trainable params: 0
    _________________________________________________________________

Apprentissage du réseau sur 6000 exemples et comparaison des performances avec le réseau dense appris dans les mêmes conditions.

train_img2 = train_img[:6000]
train_label2 = train_label[:6000]
valid_img2 = train_img2[:500] 
valid_label2 = train_label2[:500]

Entrainement du modèle

#Entrainement du modèle sur le jeu de données réduit
lenet_5_model.fit(train_img2, train_label2, epochs=5, validation_data=(valid_img2, valid_label2))

# Evaluation sur le jeu de données test
lenet_5_model.evaluate(test_img, test_label)


313/313 [==============================] - 1s 4ms/step - loss: 0.0533 - accuracy: 0.9853
[0.053335435688495636, 0.9853000044822693]

Nous remarquons d'une part que la performance du modèle sur les données de validation est de 100% et ce avant même d'atteindre la 5ème itération et d'autre part que la précision sur le jeu de données test s'est nettement améliorée (une augmentation de 0.6 point) par rapport au modèle précédent.

Dans le cas de l'apprentissage avec le réseau dense, nous avions obtenu une réduction du score de 5% en passant d'un ensemble de données de taille 50000 à un ensemble de données de taille 5000 soit une proportion de 10%. Alors que dans le cas du réseau convolutionnel, en réduisant avec la même proportion (de 60000 à 6000), nous obtenons des résultats opposés. En effet, avec le réseau convolutionnel la performance a augmenté de 0.6% même si cela reste faible. En résumé, compte tenu de la difficulté de disposer des données (coût et temps), le choix d'un modèle qui utilise moins de données d'entrainement accompagné d'une meilleure performance sera de mise. Il faut également noter que la différence de performance entre ces deux modèles devient plus grande si on tient compte du nombre d'epoques nécessaire pour avoir de tels scores sachant que le modèle dense semble prendre plus de temps d'exécution du fait du nombre d'epoques assez élevé qu'il utilise contrairement au modèle convolutionnel.

Outil utilisé : Python

License

Partager sur :

Mamoudou KOUME

Data Scientist Researcher

Je m'intéresse principalement aux Mathématiques et à l'Intelligence Artificielle dans son ensemble mais plus particulièrement au Machine Learning, à la Statistique bayésienne, au Traitement Naturel du Langage, aux processus d'optimisation (Descente de gradient, Gradient boosting...), au Traitement du signal, aux Problèmes inverses et aux Représentations parcimonieuses.